It is no secret that there is much tension in the world recently, with US and China, the two global superpowers, both slapping import tariffs on each other’s goods. This has created unfavourable business environments for some industries that are directly affected, such as steel, aluminum, beef, soy beans, semiconductors, motorcycles, cars, aerospace engineering, etc. Furthermore, the trade war, or at least the possibility of one, is surely creating a heavy fog of uncertainty, within which, investors and businesses in all sectors and industries found themselves unsure of what will happen. Uncertainty is bad for every business.

This article delves into the game theory behind a trade war and discusses some possible solutions from game theory perspective.

Abstract: In terms of international trade, China-US trade situation resembles two relevant games: Prisoner’s Dilemma and Game of Chicken. Both games have a clear optimal strategy: tariffs. Two games require two different solution strategies, and that makes it difficult for two countries to co-operate. In reality, many other factors will likely come into play, such as perception of prestige, desire to be perceived prestigiously, transparency of communication, future electability of politicians, and so on.

 

I have always been a fan of Game Theory. I believe it is highly relevant in the majority of social, socioeconomic, and political interactions. Its largest impact is, without a doubt, found on the issue of international trade. Therefore, I believe it is worthy to discuss the Game Theory mechanism behind the current looming trade war between China and US.

The most important step in Game Theory analysis is game identification. That is right: it would cause great peril if the analyst mis-identifies the game at hand, as there are many versions of games, and each game has a different payoff structure. In this case, it is quite clear that two games are relevant: Prisoner’s Dilemma and Chicken.

Prisoner’s Dilemma:

In Prisoner’s Dilemma, two prisoners (A and B) are simultaneously arrested and interrogated. The payoff structure is briefly summarized as the following:

• If A and B both cooperate, they will be given the mercy of the law. Their sentences will be 1 year, each.
• If they both defect and deny any wrongdoing, they will be given 5 years each of prison time.
• If one prisoner cooperates, but the other denies, then the prosecutor will let the prisoner who denies walk, and jails the prisoner who cooperates for a whopping 10 years.

(The payoff structure of Prisoner’s Dilemma)

 

The optimal strategy for both players is to defect and here is why:

Let’s say that you are Prisoner A: Prisoner B will either cooperate or defect, as there is no additional option. If B cooperates, it is in your best interest to defect. You will be able to walk free, as opposed to cooperate with B and be jailed for one year. If B defects, then it is in your best interest to defect as well. The difference is 5 years in prison. Therefore, regardless of the other player’s decision, each reasonable prisoner will choose to defect 100% of the time, resulting in the “Defect-Defect, 5 year-5year” payoff.

It is easy to see why it is relevant in today’s trade war. China and US are important trade partners to each other. It is beneficial to trade with low restrictions; hence, both have done so over the years. It is up for debate how low in reality those restrictions were, but that is a separate discussion for another day. However, both will gain slightly by implementing trade tariffs unilaterally, given the other country does not retaliate. If the other country retaliates, both economies will suffer. Therefore, the payoff is very similar to that of the Prisoner’s Dilemma.

I have created the following payoff structure to represent the current trade dispute between China and US. The aggregate of utility is the highest (16) under free trade (8,8). However, by implementing unilateral trade tariff, each country gains slightly while setting the other country back by a large margin (9,6). The aggregate is also smaller (15). If both countries implement trade tariffs, neither country can utilize the relative advantage of the other country, and both will be forced to produce everything domestically. The prices will be higher and the market will be smaller. It is a well known fact that both countries will suffer greatly under a highly restrictive trade environment. Therefore, I have labelled it (4,4).

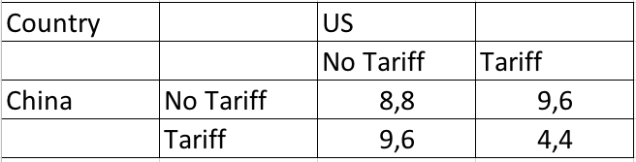
Just like the original version of Prisoner’s Dilemma, both countries have an optimal strategy of implementing tariffs. The tragic outcome seems to be inevitable. Both countries are doomed to suffer, even though, clearly, it is the worst scenario for either country.

 

Game of Chicken:

The Game of Chicken is a much more simple and interesting game. The original Game of Chicken dictates that two drivers are hurling towards each other in their respective cars. The first to swerve out is the chicken and will be mocked for the rest of his life. The winner enjoys eternal admiration from the crowd. However, both understand that it is better to be laughed at, than to crash and die. If neither swerves out of the way, yes, you guessed correctly: both will die in the crash.

In the game of chicken, there are various payoff structures that share the same essence. Depending on the degree to which one resents humiliation and cherishes life (as long as he/she still values life more than he hates humiliation), the numbers assigned will be different. However, the numbers, as long as do not change the overall payoff structure, are of little importance. I have created the following payoff scheme:

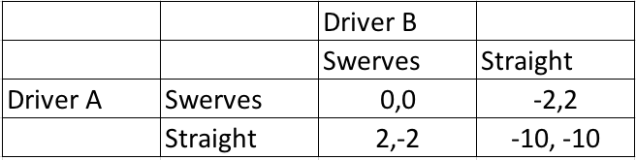
The game has a negative aggregate payoff, meaning that more harm than good comes from this game. It is clearly nice for the two players to talk it out before having the dual of death.

However, that is not the optimal strategy. The Game of Chicken has an optimal strategy that is hard to detect, but it does have one. It is optimal for a given player to take off the wheel in his car, and throw it out for the other player to see.

In a Game of Chicken, it is optimal for a given player to take off the wheel in his car and throw it out for the other player to see.

The crucial detail is that the other player not only must see it but also understand that you are now unable to swerve. You have now singlehandedly changed payoff of the game.

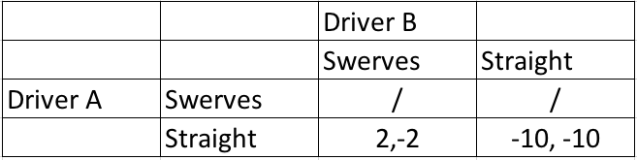
In the new payoff structure, driver A is unable to swerve as he does not have the wheel. Driver B understands that Driver A is unable to swerve. Therefore, in the new game, Driver A does not have the option to swerve. Driver B must either live and be the chicken, or die with A. The option is clear enough: Driver B swerves (or gives up). Both are alive. A wins.

Therefore, the first person to throw out the wheel for the other driver to see is the winner. It is called the Madman Strategy. No one wants to play Chicken with someone crazy.

The trade war between US and China is in large part similar to the Game of Chicken. Both parties understand that with tariffs, the consequences will be dire. Either power hopes that the other country will be the chicken on the international stage. The chicken is punished by the humiliation that comes from being only the second most powerful country in the world and losing the mano-a-mano battle.

 

Iterations:

The presence of iterations in Game Theory is crucially important. It changes the payoff structure by adding another dimension to the game: expectations.

In the game of Prisoner’s Dilemma, if the prisoner who defects has other consequences, then he will choose to cooperate. As the popular saying goes, “Snitches get stitches.” If a prisoner knows that he will be executed on the street because he has violated this sacred rule, he will not confess. In this new game, the prisoner will estimate the probability of himself being killed for snitching. If the probability weighted consequence is bad enough (Prob. of being killed * The payoff assigned to death), the prisoner will reasonably choose to cooperate with the other prisoner.

Similar to such a change, many factors can now come into play:

1. The probability of his family members being killed by gang members as punishment for his confession/defection.
2. The probability of him losing street credibility, or trust.
3. The payoff that is related to losing street credibility or trust.

Therefore, in an iterated game of Prisoner’s Dilemma, by temporarily choosing the option that allows for the highest aggregate payoff, the player creates a stable environment that allows for other players to expect the highest aggregate payoff to occur, even though that this is not the optimal strategy for either player. 

 

In the game of Chicken, however, if the player allows himself to be the chicken for once, he will be repeatedly taken advantage of in an iterated version. Expectations are created that Driver A is weak and afraid. Driver B can repeatedly force A to swerve. Oppositely, if A is proven to be insane (not brave, but clinically insane). B will be the chicken over and over again.

Therefore, we see that iterations in the Prisoner’s Dilemma makes the both players more cooperative, but iterations in the Game of Chicken put even more pressure on the players to act insanely.

 

Solutions and Other Factors:

As we have established that the two games are relevant and both have distinct strategies, the possible solution is to allow for iterations for the Prisoner’s Dilemma, and not allow iterations for the Game of Chicken.

Two things must be accomplished:

1. China and US must come together and formulate a long-term trade vision. It does not have to be legally binding. However, it is important to reassure each other that the game will continue. If one country defects, the aggregate payoff will be continuously low.
2. At the same time, international regulations must become stronger. Any further act of taunting and challenging to a Game of Chicken should be punished.

Therefore, the Prisoner’s Dilemma is allowed to continue with iterations, and the Chicken game is banned forever.

 

In reality, numerous other factors come into play and affect the outcome of the game:

1. It is wrong to view China and US as two independent entities. On the micro level, the decision makers may have incentives that are different from the incentive of the whole country overall. On this note, Xi Jinping’s incentives are more or less now closer to those of the country, as he does not face any election pressure and he has an unlimited term. On the other hand, Trump and the Republicans face pressure of re-election. Therefore, he has the incentive to go fully insane to build a reputation of being tough on China among the American people. He has a greater upside than the US does as a country. Being the decision maker, he will change the payoff structure of the game.
2. It is also not safe to assume that the real game is as transparent as the ones in theory. In theory, both players act at the same time and both players have the perfect information about the game and the other player. In reality, this is a very dangerous assumption to make. China does not have perfect information on what the US wants to achieve. China is not sure that the US will not be willing to sacrifice itself to cause a greater damage on China. This is called relative victory. US is not sure what information China has, therefore, it allows the possibility of bluff, on both sides.

 

As we can see that the real game is much messier than the game in theory, much like anything else in life. The essence is similar, however, that neither country will back down unless revolutionary institutional changes occur on an international scale, to prevent countries to unilaterally implementing tariffs. But again, is that moral? Better yet, is that legal? That is for a whole another discussion.